| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Charge Carriers
- 서울 자치구별 경찰서
- Density Of states function
- Diffusion Current
- 생성(Generation)
- Semiconductor
- Scattering
- 물리전자
- 앰비폴러 전송 방정식
- 파동 함수
- 캐리어 농도
- 에너지밴드
- 유효질량
- 과잉 캐리어
- KANC
- Mobility
- Ambipolar transport equation
- 반도체공학
- 한국나노기술원
- 재결합(Recombination)
- Energy Band
- Wave Function
- neamen
- Fermi Energy Level
- 페르미 에너지 준위
- 나노분석평가
- Drift Current
- 확산 전류
- Excess Carrier
- 서울 경찰서 위도/경도
- Today
- Total
읽고 기록하는 삶
[물리전자] 4.5 전하 중성 조건(Charge Neutrality) 본문
CHAPTER 4
The Semiconductor in Equilibrium
들어가며
우리는 Chapter 4.3.1에서 이미 불순물 반도체(Extrinsic Semiconductor)의 경우에 대한 캐리어 농도를 구한 적 있습니다.
오늘은 전하 중성 조건(Charge Neutrality) 을 활용하여 불순물 반도체의 캐리어 농도에 대해 알아보겠습니다.
4.5.1 Compensated Semiconductors Charge Neutrality
먼저, 두 가지 개념에 대해 알고 가겠습니다.
첫번째, 전하 중성 조건(Charge Neutrality Condition)에 대해 간단히 알아보겠습니다.
열평형 상태의 반도체 내부에는 수많은 캐리어가 상호작용하지만 전체적으로 볼 때, 전기적으로 중성인 것을 뜻합니다.
(The electrons are distributed among the various energy states, creating negative and positive charges, but the net charge density is zero)
두번째, 보상 반도체(Compensated Semiconductors)에 대한 개념입니다.
보상 반도체(Compensated Semiconductors)는 도너(Donor)와 억셉터(Acceptor)가 모두 존재하는 반도체를 의미합니다.
이러한 반도체는 MOSFET과 같은 반도체 소자의 제조 과정에서 자연스럽게 발생하게 됩니다.
(예를 들면, n-type substrate에 p-well을 구성하거나, p-type substrate에 n-well을 구성하는 경우가 있을 수 있죠.)
| No. | 구분 | 물질 | 도펀트 | 도펀트 농도 |
| 1 | n형 보상 반도체 (n-type compensated semiconductor) |
n-type material | Acceptor | Nd > Na |
| 2 | p형 보상 반도체 (p-type compensated semiconductor) |
p-type material | Donor | Nd < Na |
| 3 | 완전 보상 반도체 (Completely compensated semiconductor) |
n-type material | Acceptor | Nd = Na |
| p-type material | Donor | Nd = Na |
에너지 밴드 다이어그램으로 표현하면 아래와 같습니다.
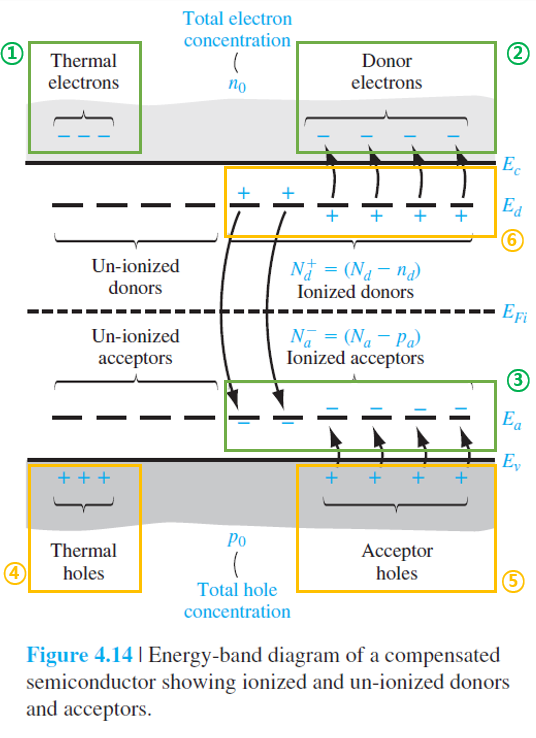
4.5.2 Equilibrium Electron and Hole Concentration
그렇다면 전하 중성 조건(Charge Neutrality Condition)은 어떻게 표현할 수 있을까요?
전하 중성 조건은 전체 시스템의 순 전하(Net Charge)가 '0' 인 상태인 것을 의미하므로 다음과 같이 표현할 수 있습니다.
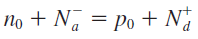
또는, 다음과 같이 표현할 수도 있습니다.

식 (4.56)은 Figure 4.14에서의 초록색 박스(①+②+③)와 노란색 박스(④+⑤+⑥)로부터 도출된 것입니다.
이제, 도펀트 원자(Dopant atoms)가 완전 이온화(Complete Ionization)된다고 가정하면 결론을 얻을 수 있습니다.
즉, 도너 전자(nd)와 억셉터 정공(pa)은 모두 '0' 이므로, 다음과 같이 표현할 수 있습니다.

Chapter 4.3.1 마지막에서 다룬 관계식을 식 (4.58)에 대입하면 전자의 농도에 대한 2차 방정식을 얻을 수 있습니다.


식 (4.59b)에 대하여 근의 방정식을 사용하면, 평형 상태일 때, 불순물 반도체의 전자의 농도를 구할 수 있습니다.

동일한 방법으로 평형 상태일 때, 불순물 반도체의 정공의 농도를 구하면 다음과 같습니다.

위의 식 (4.60)과 식 (4.62)는 도핑 농도에 따라 수식을 근사화하여 계산할 수 있습니다. ( 예제 4.9 )
이제 우리는, 열평형 상태에서의 불순물 반도체의 캐리어의 농도를 구할 때, 두 가지 방법을 이용할 수 있습니다.

마지막으로, 온도에 따른 불순물 반도체(Extrinsic Semiconductor)의 전자의 농도 변화 그래프를 보겠습니다.
진성 캐리어 농도(ni)는 온도와 관련된 함수입니다. 즉, 온도가 증가할수록 진성 캐리어 농도도 증가합니다.

| No. | 구간(온도) | 설명 |
| 1 | Partial Ionization Region(~100K) | 완전 이온화 될 때까지, 이온화 정도에 따라 전자의 농도가 기하급수적으로 증가 |
| 2 | Extrinsic Region(100K~500K) | 완전 이온화 후, 온도에 따른 ni의 증가량이 작아 전자의 농도 변화는 거의 없음 |
| 3 | Intrinsic Region(500K~) | 온도에 따른 ni의 증가량이 지배적으로 증가하여 전자의 농도가 증가 |
실제로, 온도 변화에 따른 소자의 전기적 특성을 안정적으로 하기 위해 Extrinsic Region을 만족하도록 도핑합니다.
마치며
오늘은 전하 중성 조건(Charge Neutrality) 에 대해 알아보았습니다.
다음 글에서는 페르미 에너지 준위(Fermi Energy Level)에 대해 조금 더 알아보겠습니다.
감사합니다.
읽어보면 도움 되는 포스팅
2022.11.23 - [Semiconductor] - [물리전자] 4.1.3 진성 캐리어 농도 (The Intrinsic Carrier Concentration)
2022.11.26 - [Semiconductor] - [물리전자] 4.3.1 평형 상태일 때 불순물 반도체의 캐리어 농도 (The Extrinsic Semiconductor)
'Semiconductor > Device Physics' 카테고리의 다른 글
| [물리전자] 5.1.1 표류 전류 밀도(Drift Current Density) (1) | 2022.12.05 |
|---|---|
| [물리전자] 4.6 페르미 에너지 준위의 위치(Position of Fermi Energy Level) (0) | 2022.12.02 |
| [물리전자] 4.4.2 완전 이온화(Complete Ionization)와 동결(Freeze-Out) (0) | 2022.11.29 |
| [물리전자] 4.3.4 축퇴, 비축퇴 반도체(Degenerate and Nondegenerate Semiconductors) (0) | 2022.11.29 |
| [물리전자] 4.3.1 평형 상태일 때 불순물 반도체의 캐리어 농도 (The Extrinsic Semiconductor) (0) | 2022.11.26 |




