| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Excess Carrier
- Scattering
- 물리전자
- 나노분석평가
- Density Of states function
- 파동 함수
- Drift Current
- Energy Band
- 서울 경찰서 위도/경도
- 과잉 캐리어
- 앰비폴러 전송 방정식
- 한국나노기술원
- Diffusion Current
- Fermi Energy Level
- 확산 전류
- 에너지밴드
- 서울 자치구별 경찰서
- Wave Function
- 재결합(Recombination)
- Ambipolar transport equation
- 캐리어 농도
- 생성(Generation)
- Semiconductor
- Charge Carriers
- KANC
- 페르미 에너지 준위
- neamen
- 유효질량
- Mobility
- 반도체공학
- Today
- Total
읽고 기록하는 삶
[물리전자] 2.2.2 파동 함수의 물리적 의미(Physical Meaning of the Wave Function) 본문
[물리전자] 2.2.2 파동 함수의 물리적 의미(Physical Meaning of the Wave Function)
늦더라도 확실하게 2022. 8. 7. 21:32CHAPTER 2
Introduction to Quantum Mechanics
2.2.2 Physical Meaning of the Wave Function
이번 포스트는 파동 함수의 물리적 의미에 대해서 간단하게 살펴보겠습니다.
저번 포스트에서 Crystal 안의 단 하나의 전자에 대한 거동을 묘사하기 위해 파동 함수 ψ(x,t)를 알아보았습니다.
그렇다면, 정확하게 파동 함수 ψ(x,t)와 전자 사이에는 어떤 관계를 가지고 있을까요?
즉, 다시 말씀드리자면, 복소 함수인 ψ(x,t)가 어떤 물리적인 정보를 가지고 있을까요?
지난 시간에 다뤘던 것처럼, 파동 함수 ψ(x,t)를 position-dependent와 time-dependent 함수의 곱으로 나타내면 다음과 같습니다.
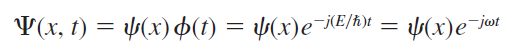
1926년, 막스 보른(Max Born)은 복소 함수 ψ(x,t)에 대해 다음과 같이 정의하여 전자의 발견 가능성을 확률 밀도로 표현하였습니다.

위의 식은 특정 시간 그리고 1차원 상의 임의의 공간 x와 x+dx 사이에서 전자가 발견될 확률이라는 것을 의미합니다.
수학적으로는 확률 밀도 함수는 파동 함수와 파동 함수의 켤레 복소수의 곱으로 표현합니다.
이를 다음과 같이 정리하여 표현할 수 있습니다.


식 (2.17)을 보시게 되면, 확률 밀도 함수는 시간에 대해 독립적이라는 것을 확인할 수 있습니다.
이러한 것을 바탕으로, 고전 역학과 양자 역학의 가장 큰 차이점을 설명 말씀드리면 다음과 같습니다.
고전 역학에서는 입자의 위치에 대해 정확히 표현할 수 있지만, 양자 역학에서는 입자의 위치가 확률로 표현된다는 것입니다.
이 책의 저자는 time-independent한 파동 함수에 대해 다루고 있습니다.
따라서, 다음 포스트에서 다룰 예시들, 더 나아가 일반적인 파동 함수에 대해 time-independent한 파동 함수에 대해 다루겠습니다.
다음 포스트에서는 경계 조건(Boundary Condition)에 대해 알아보겠습니다.
감사합니다.
'Semiconductor > Device Physics' 카테고리의 다른 글
| [물리전자] 2.3.1 자유 공간에서의 전자의 거동(파동방정식 예제1) (0) | 2022.08.12 |
|---|---|
| [물리전자] 2.2.3 경계 조건 (Boundary Conditions) (0) | 2022.08.12 |
| [물리전자] 2.2 슈뢰딩거의 파동 방정식(Schrodinger's Wave Equation) (0) | 2022.07.27 |
| [물리전자] 2.1.3 양자역학의 기본 개념(The Uncertainty Principle) (0) | 2022.07.27 |
| [물리전자] 2.1.2 양자역학의 기본 개념(Wave-Particle Duality) (0) | 2021.04.01 |




