[물리전자] 6.4 준 페르미 준위 에너지(Quasi-Fermi Energy Levels)

CHAPTER 6

Nonequilibrium Excess Carriers in Semiconductors

 

들어가며

 

오늘은 간략하게 준 페르미 에너지 준위(Quasi-Fermi Energy Levels)에 대해 알아보겠습니다.

이미 지난 글(4.1.4 / 4.6)에서 평형 상태일 때의 페르미 준위에 대한 내용을 다룬 적 있습니다. 기억 나시나요?

오늘 내용은 반도체 내 과잉 캐리어(Excess carrier)가 생성되었을 때의 페르미 준위에 대한 내용입니다.

그럼, 페르미 에너지 준위(Fermi Energy Levels)에 대한 정의를 상기하며 시작하겠습니다.

 

페르미 에너지 준위(E_F)란?
 : the energy below which all states are filled with electrons and above which all states are empty at T=0K.

 

 

 

4.6 Posotion of Fermi Energy Level

 

먼저, 용어에 대한 의미에 대해서 생각해보고 가겠습니다. 왜, 준(Quasi-)이라는 말이 붙었을까요?

페르미 에너지 준위(Fermi Energy Level)라는 건 에너지 밴드 다이어그램에서 표현했을 때 하나의 연결된 선입니다. 

그러나, 반도체 내 과잉 캐리어(Excess carrier)가 생성되었을 때 당연히 순간적으로 페르미 에너지 준위가 변화하게 됩니다.

이 때, 하나의 연결된 선으로 표현되지 않습니다. 즉, 엄밀하게는 페르미 에너지 준위(Fermi Energy Level)은 아닙니다.

그럼에도 반도체 내 과잉 캐리어(Excess carrier)가 생성 됐을 때의 상황을 표현하기 위해 '준(Quasi)'을 붙인 겁니다.

 

 

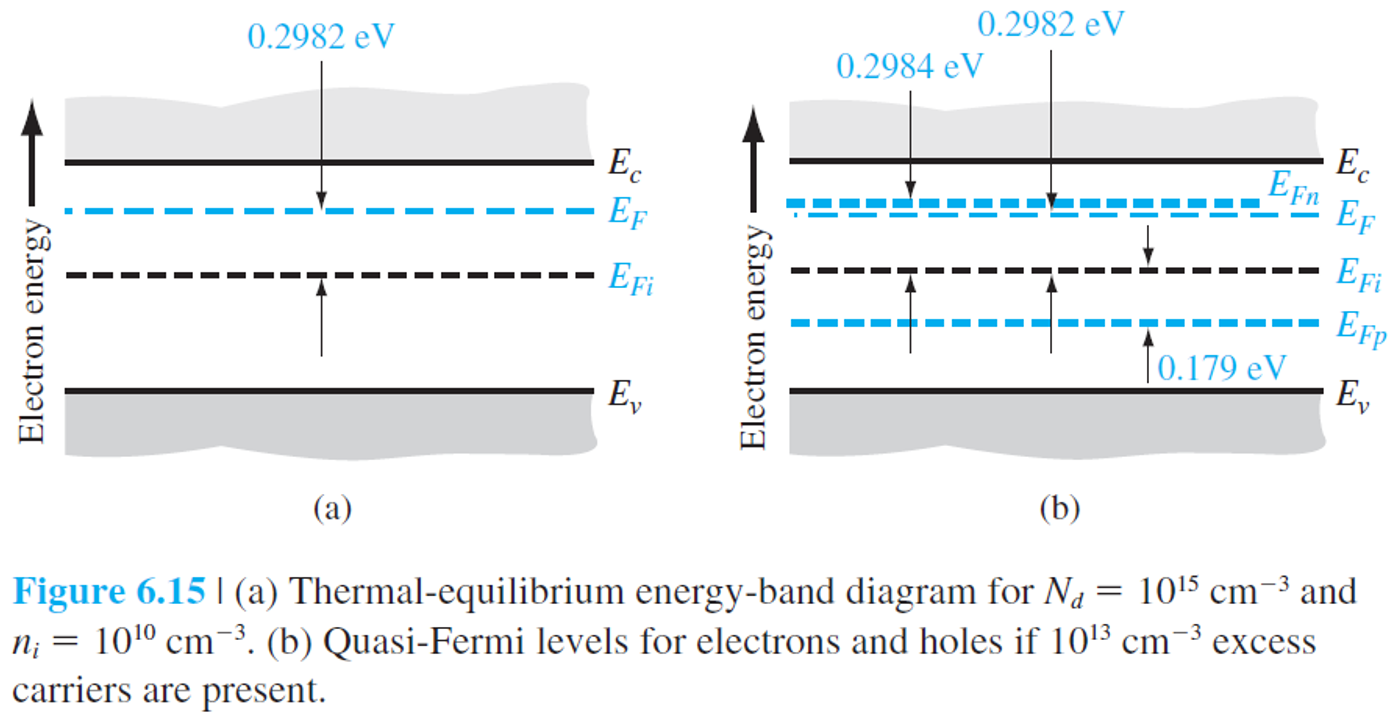
좌측 그림은 평형 상태에서의 에너지 밴드 다이어그램, 우측 그림은 과잉 캐리어 발생시 에너지 밴드 다이어그램입니다.

참고로 과잉 캐리어가 동일하게 발생해도 상대적으로 소수 캐리어인 정공의 변화가 큰 것을 확인할 수 있습니다.

 

정확하게 구하는 수식은 아래와 같습니다. 자세한 내용은 EXAMPLE 6.7을 참조하시면 이해에 도움이 될 것입니다.

 

식 (6.85a)

 

식 (6.85b)

 

 

마치며

 

오늘은 정말 간략하게 준 페르미 에너지 준위(Quasi-Fermi Energy Levels)에 대해 알아보았습니다.

준(Quasi-)에 대한 이해만 하신다면, 에너제 밴드 관련 내용은 이미 다뤘기 때문에 비교적 이해하기 수월하실 거라 생각합니다. 

다음 글에서는 Shockley-Read-Hall(SRH) 재결합에 대해 알아보겠습니다.

 

감사합니다.

 

읽어보면 도움 되는 포스팅

 

 

2022.11.23 - [Semiconductor/Device Physics] - [물리전자] 4.1.4 진성 페르미 준위의 위치 (The Intrinsic Fermi-Level Position)

2022.12.02 - [Semiconductor/Device Physics] - [물리전자] 4.6 페르미 에너지 준위의 위치(Position of Fermi Energy Level)