| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Ambipolar transport equation
- Charge Carriers
- 에너지밴드
- 앰비폴러 전송 방정식
- KANC
- Diffusion Current
- 파동 함수
- 서울 경찰서 위도/경도
- 물리전자
- 과잉 캐리어
- Fermi Energy Level
- 한국나노기술원
- 유효질량
- Density Of states function
- 나노분석평가
- Scattering
- 확산 전류
- 반도체공학
- Excess Carrier
- Semiconductor
- Mobility
- 재결합(Recombination)
- Wave Function
- Drift Current
- neamen
- 서울 자치구별 경찰서
- 생성(Generation)
- Energy Band
- 캐리어 농도
- 페르미 에너지 준위
- Today
- Total
읽고 기록하는 삶
[물리전자] 3.1.1 에너지 밴드(Energy Band)의 형성 본문
CHAPTER 3
Introduction to The Quantum Theory of Solids
3.0 Preview
우리는 지금까지 Chapter 1, Chapter 2를 통해 전자에 대해 기술하는 여러 방법에 대해 알아보았습니다.
슈뢰딩거의 파동 방정식을 다양한 조건에서 풀어보며 Particle의 에너지가 양자화(Quantization)되어 있음을 알았습니다.
Chapter 3에서는 앞서 다룬 내용을 기반으로 Crystal Lattice 내의 무수히 많은 전자들에 대해 다뤄볼 것입니다. 이번 챕터를 마치게 되면 우리는 Crystal Lattice 내에서의 전자들의 특성을 알 수 있고, 통계적 방법을 통해 전자를 표현할 수 있을 것입니다.
3.1.1 Formation of Energy Bands
물리전자에서 정말 중요한 개념인 에너지 밴드에 대해서 먼저 알아보겠습니다. 아래 사진부터 보겠습니다.
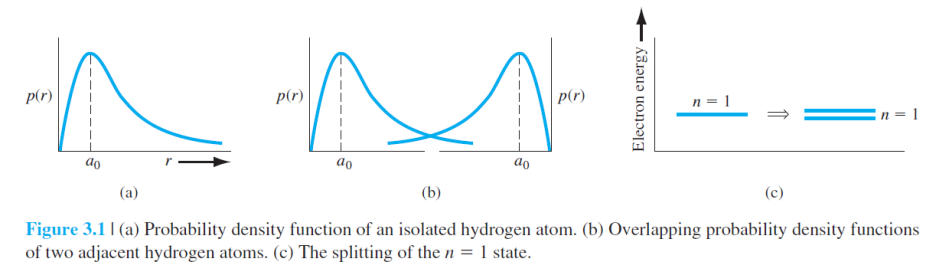
Figure 3.1a는 수소 원자일 때, 가장 낮은 에너지 상태에서의 전자가 존재할 확률 밀도 함수를 의미합니다.
*
Chapter 2에서 다루지 않고 넘어와서 조금은 낯설게 느껴지실 수 있습니다.
우리는 Chapter 2에서 파동 방정식을 일차원 직교 좌표계에서만 다뤘었죠. Chapter 2의 끝부분에 3차원 구형 좌표계에서 전자가 존재할 확률 밀도 함수에 대해서 다루는 부분이 있으니, 참고하시면 Figure 3.1a가 어떻게 나왔는지 확인하실 수 있습니다.
*
한편, Figure 3.1b는 서로 다른 두 원자가 매우 가까울 때 확률 밀도 함수가 겹치는 상황인 것을 나타냅니다.
즉, 다시 말하면 전자가 서로 상호 작용을 할 수 있음을 의미하는 것이죠.
이러한 상호 작용은 파울리의 배타 원리(Pauli exclusion principle)에 의해 에너지 레벨이 Figure 3.1c 처럼 나뉩니다.

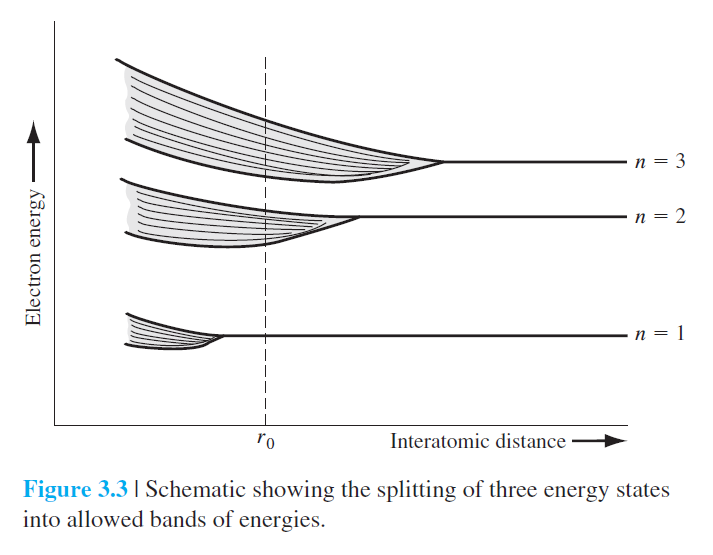
위의 Figure 3.2, Figure 3.3을 보며 더 자세히 알아보겠습니다.
Figure 3.2는 에너지 준위가 나뉘는 모습을 표현한 모습이고, Figure 3.3은 에너지 준위를 더 많이 표현했을 때의 모습입니다.
여기서, r0 는 평형 상태일 때의 원자간 거리(Equilibrium interatomic distance)를 의미합니다.
r0에서 전자가 존재할 수 있는 에너지 밴드가 있고, 이 에너지 밴드는 모두 불연속적 준위로 나뉘어져 있습니다.
즉, 파울리 배타 원리(Pauli exclusion priciple)에 의해 각각의 전자들은 모두 다른 에너지 준위를 가지며 존재하게 됩니다.
쉽게 예시를 들어 설명하면 다음과 같습니다.
10^19개의 전자로 이루어진 원자에 대해 생각해보겠습니다. r0에서 허용 에너지 밴드(the allowed energy band)가 1eV라고 가정할 때, 10^19개의 전자들은 1eV 내에서 파울리 배타 원리에 위배되지 않기 위해 에너지 밴드를 10-19eV의 에너지 준위로 쪼개어 존재합니다. 이 때, 10^-19eV의 에너지 준위는 매우 작기 때문에 연속적으로 분포한다고 가정합니다. (quasi-continuous distribution)
다시 Figure 3.3을 볼까요? 이번엔 n=3 일 때에 대해서 알아보겠습니다. 방법은 동일합니다.
다만, n이 클수록 에너지 밴드가 더 일찍 형성된다는 차이가 있습니다.
또한, Figure 3.3에서와 같이 에너지 밴드가 형성되었다고 할 때, Figure 3.4b와 같이 전자가 존재할 수 없는 부분이 존재합니다.
지금까지 다뤘던 내용을 실리콘 원자를 예시로 하여 다시 말씀드리면 아래와 같습니다.
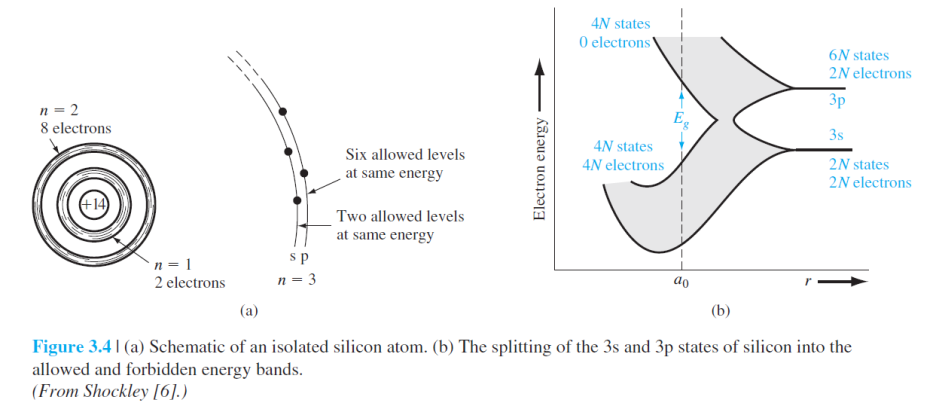
Figure 3.4a는 실리콘 원자에 대해 표현한 그림입니다.
하나의 실리콘 원자에는 총 14개의 전자가 존재하며, 그 중 10개는 원자핵과 비교적 가까운 곳에 위치하여 존재합니다.
원자가 전자(Valence electrons)라는 나머지 4개의 전자들이 상대적으로 약한 결합을 가지며 다양한 화학 반응에 참여합니다.
Figure 3.4b를 보면, a0 로 가까워질수록 3s state와 3p state들은 서로 상호 작용하며 겹치게 되며, 다시 에너지 밴드를 형성합니다. 이 때, 절대 영도를 기준으로 4개의 원자가 전자는 에너지 준위가 낮은 밴드(the valence band)에 모두 존재하고, 에너지 준위가 높은 밴드(the conduction band)에는 존재하지 않으며, 이 에너지 밴드의 폭을 에너지 밴드 갭(Energy band gap)이라고 합니다.
오늘은 물리전자에서 정말 중요한 개념인 에너지 밴드의 형성과 의미를 알아보았습니다.
이 개념은 앞으로 다루게 될 Crystal 의 전기적 특성을 다룰 때 매우 요긴하게 사용될 개념입니다.
다음 글에서는 오늘 다룬 내용을 바탕으로 반도체 소자에서 전기적 특성을 기술하는 방법에 대해 다루겠습니다.
긴 글 읽어주셔서 감사합니다!
'Semiconductor > Device Physics' 카테고리의 다른 글
| [물리전자] 3.2.2 표류 전류(Drift Current) (0) | 2022.10.13 |
|---|---|
| [물리전자] 3.2.1 에너지 밴드와 원자가 결합 이론(The Bond Model) (0) | 2022.10.12 |
| [물리전자] 2.3.3 터널링 효과(The Tunneling Effect) (1) | 2022.08.21 |
| [물리전자] 2.3.2 무한 전위 우물에서의 전자의 거동(파동방정식 예제2) (0) | 2022.08.13 |
| [물리전자] 2.3.1 자유 공간에서의 전자의 거동(파동방정식 예제1) (0) | 2022.08.12 |




