[물리전자] 2.3.3 터널링 효과(The Tunneling Effect)

 

CHAPTER 2

​

Introduction to Quantum Mechanics

 

2.3.3 The Step Potential Function

지난 글에서는 무한 전위 우물(The Infinite Potential Well)에 대해서 알아보았는데요.

오늘은 아래의 Figure 2.8에 대한 문제에 대해 풀어보겠습니다. 이 문제를 풀면서 터널링에 대한 개념도 함께 알아보겠습니다!

 

Figure 2.8 The step potential function

 

이전과는 달리, RegionⅠ에서 RegionⅡ를 지나는 입자의 거동에 대한 문제입니다.

주어진 상황만 달라졌을뿐, 접근 방법은 동일합니다. 즉, time-independent wave equation를 각 영역에서 풀면 됩니다.

 

1) Region Ⅰ

Region Ⅰ에서 V=0이므로 파동 방정식은 다음과 같이 정리할 수 있습니다.

식 (2.40) Region Ⅰ에서의 파동 방정식

또한, 우리는 이미 다뤘던 내용을 통해 위의 방정식의 해가 다음과 같다는 것을 알고 있습니다.

식 (2.41) Region Ⅰ에서의 일반해

위의 방정식에서 첫 번째 항은 초기의 입자가 +x 방향으로 운동하고 있는 것을 나타내고, 두 번째 항은 반사된 입자가 -x 방향으로 운동하고 있는 것을 나타냅니다. 이 때, A1 * A1*은 초기 상태의 입자에 대한 확률 밀도 함수를 의미합니다. 한 편, 초기 상태의 입자의 속도를 vi 라고 한다면, 초기 상태의 입자에 대한 Flux는 vi  * A1 * A1*로 표현할 수 있습니다.

 

같은 방법으로, 반사된 입자에 대한 Flux는 vr  * B1 * B1*로 표현할 수 있습니다. 이 내용은 마지막 부분에서 활용되니 참고해주세요!

 

2) Region Ⅱ

Region Ⅱ에서 V=0이므로 파동 방정식은 다음과 같이 정리할 수 있습니다.

식 (2.43) Region Ⅱ에서의 파동 방정식

위의 방정식 또한 전형적인 미분방정식의 형태이므로, 다음과 같은 일반해가 나온다는 것을 알 수 있습니다.

식 (2.44) Region Ⅱ에서의 일반해

 

각 영역에 대한 파동 방정식을 도출했으니, 경계 조건(Boundary Condition)을 활용하여 미지수를 최대한 줄이면 됩니다.

먼저, 식 (2.44)의 두 번째 항을 보면, x가 증가함에 따라, 무한히 증가하는 함수임을 알 수 있습니다.

파동 함수는 유한 함수이므로, B2=0이라는 것을 알 수 있습니다.

(식 2.46)

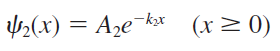
한편, x=0에서 파동 함수는 연속이므로, 다음과 같은 관계식을 얻을 수 있습니다. (∵ ψ1(0)=ψ2(0) )

식 (2.48)

또한, 주어진 파동 함수는 모든 영역에서 유한하므로, 다음과 같은 조건을 활용하여 새로운 관계식을 얻을 수 있습니다.

식 (2.49)

식 (2.50)

지금까지 도출된 두 관계식을 활용하여, 각 파동함수의 상수들을 A1을 활용하여 표현하면 다음과 같습니다.

식 (2.51a)

식 (2.51b)

 

위에서 잠깐 언급했었던 내용 기억하시나요? 초기 상태의 Flux와 반사된 Flux에 대한 내용이었습니다.

관련하여 반사 계수(Reflection coefficient)에 대해 정의를 할 수 있는데요, 간단히 말하면 들어간 Flux 대비 반사된 Flux입니다.

식 (2.53) Reflection Coefficient

 

이제 Region Ⅰ에서의 반사 계수를 알아보겠습니다. 즉, +x 방향으로 거동하는 입자가 계단 전위(Step Potential)를 만났을 때의 상황입니다.

Region Ⅰ에서는 V=0이므로, 거동하는 입자의 에너지는 운동에너지 밖에 없는 것을 알 수 있습니다. 즉, 다음과 같습니다.

식 (2.54) Kinetic Energy

이러한 조건을 활용하여 Wave Number k1을 다시 표현하면 다음과 같습니다.

식 (2.55)

이를 다시 vi,vr로 표현하면 다음과 같습니다.

식 (2.56)

식 (2.57)

 

입사된 입자와 반사된 입자의 속도는 같으므로, 아래의 표현처럼 반사계수의 값은 1 인 것을 확인할 수 있습니다.

식 (2.59)

이것이 어떤 것을 의미할까요?

전위 장벽이 V0 이고, 거동하는 입자가 V0보다 작은 에너지로 장벽을 지날 때, 그 에너지 장벽을 뚫고 넘어가는 것이 없다는 것을 의미합니다. 이러한 내용은 고전 역학(classical physics)와 일치하는 것을 알 수 있습니다. 그러나, 한 가지 이상한 점이 있습니다.

 

식 (2.46)을 보시면, x>0일 때의 파동 함수가 정의되어있고, A2 또한 0이 아닌 것을 알 수 있습니다.

즉, Region Ⅱ에서 확률 밀도 함수가 0이 아니라는 것을 의미하고, 이는 Region Ⅱ에서 전자가 발견될 확률이 있다는 것을 의미합니다. 이는 입사되는 입자가 전위 장벽을 뚫고 RegionⅡ로 넘어갈 수 있다는 것을 의미하고, 이것이 바로 고전 역학과 양자역학의 차이입니다.

 

터널링의 개념은 물리전자에서 매우 중요한 개념입니다.

이후에 다루게 될 MOS 구조, MOSFET, 더 나아가 메모리와 관련된 내용을 다룰 때 터널링에 대한 내용은 개념을 이해하는데 반드시 필요합니다. 꼭 이해하고 넘어가시면 좋겠습니다.

 

다음 포스트는 Chapter 3에 대해 하나씩 다뤄보겠습니다.

긴 글 읽어주셔서 감사합니다.