| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- Fermi Energy Level
- Mobility
- Wave Function
- Ambipolar transport equation
- 나노분석평가
- neamen
- 재결합(Recombination)
- Drift Current
- Charge Carriers
- 유효질량
- 페르미 에너지 준위
- 캐리어 농도
- Scattering
- 서울 자치구별 경찰서
- 반도체공학
- 한국나노기술원
- 과잉 캐리어
- 확산 전류
- 파동 함수
- Density Of states function
- Diffusion Current
- Excess Carrier
- KANC
- 물리전자
- Energy Band
- 생성(Generation)
- Semiconductor
- 서울 경찰서 위도/경도
- 에너지밴드
- 앰비폴러 전송 방정식
- Today
- Total
읽고 기록하는 삶
[물리전자] 3.4.1 상태 밀도 함수(Density Of States Function) 본문
[물리전자] 3.4.1 상태 밀도 함수(Density Of States Function)
늦더라도 확실하게 2022. 11. 3. 20:49
CHAPTER 3
Introduction to The Quantum Theory of Solids
3.4 Density Of States Function
지금까지 우리는 에너지 밴드의 정의와 형성되는 원리, 그리고 에너지 밴드 구조에 따른 전기적 특성에 대해 알아봤습니다.
이전에도 언급하였듯이, 우리는 반도체 소자의 전류-전압 특성(Current-Voltage Characteristic)을 아는 것이 목표입니다.
그렇기 때문에 전류 특성을 파악하기 위해 Carrier(Electron or Hole)의 거동을 파악하는 것이 매우 중요합니다.
오늘은 Carrier의 거동을 파악하기 위해 필요한 상태밀도함수(Density of States Function)에 대해 알아보겠습니다.
상태밀도함수(Density of States Function)란 무엇일까요?
상태밀도함수란 단위 부피당, 단위 에너지당 전자가 존재할 수 있는 양자 상태(Available Quantum states)의 수를 의미합니다.
예전에, 3.1절에서 파울리의 배타 원리에 의해 하나의 전자는 하나의 양자 상태(Quantum state)만을 가질 수 있으며,
그러한 이유로 에너지 밴드는 불연속적 준위(Discrete Energy Level)를 갖는다고 말씀드렸습니다.
즉, 상태밀도함수는 얼마큼의 허용 에너지 상태(allowed energy states)를 갖는지를 의미하며 수식은 다음과 같습니다.
3.4.1 Mathematical Derivation
상태밀도함수를 수학적으로 유도하기에 앞서, 전자는 3차원 무한 전위 우물 내에서 거동하는 자유 전자라고 가정하겠습니다.
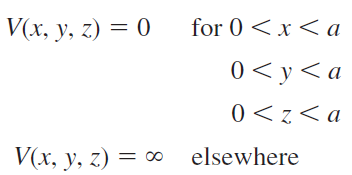
슈뢰딩거의 파동 방정식에서 현재 조건을 활용하여 정리하면 다음과 같습니다.
(2.3.1절에서 다뤘던 1차원 무한 전위 우물 내에서의 파동 방정식 예제를 참고 바랍니다.)

k는 파수(wave number)를 의미하며, n은 양자수(quantum number)를 의미합니다.
(유도 과정 첨부하오니, 필요하신 분만 참고 바랍니다.)

위에서 얻은 식 (3.60)을 활용하여 k-space 에 존재하는 허용 양자 상태(the allowed quantum states)를 표현할 수 있습니다.
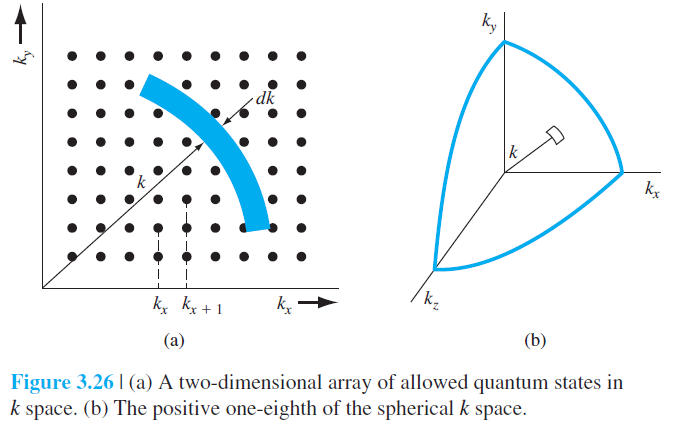
먼저 위의 그림을 볼까요?
Figure 3.26a 는 그러한 양자 상태를 k_x,k_y 에 대한 2차원 평면에 나타낸 것입니다.
각각의 점들은 전자가 존재할 수 있는 양자 상태를 의미하며, 이는 전자의 에너지에 의해 결정됩니다. (n_x , n_y, n_z)
Figure 3.26b는 식 (3.60)에 대한 제 1 팔분공간을 표현한 것입니다.
(참고로, k_x, k_y, k_z, n_x , n_y, n_z 의 부호는 전자가 존재할 확률 관점에서 동일하므로 양수든 음수든 다른 양자 상태를 의미하지 않습니다.)
이제 우리는 단위 부피당 양자 상태(the allowed quantum states)가 얼마나 존재하는지 알고 싶습니다.
위의 내용을 바탕으로 양자 상태(Quantum states)의 미소 밀도(differential density)에 대해 표현해보겠습니다.

식 (3.61)은 k_x 방향에서의 두 양자 상태 사이의 거리를 의미합니다. (Figure 3.26a 참조)
이를 3차원 공간으로 확장하여 표현하면 다음과 같습니다.

식 (3.62)는 3차원 공간 상에서 하나의 양자 상태가 갖는 부피(the volume of a single quantum state)를 의미합니다.
한편, Figure 3.26b에서 볼 수 있듯이, 3차원 공간에서의 미소 부피(differential volume)는 4πkdk 입니다.
따라서, k-space 에서의 양자 상태의 미소 밀도(the differential density of quantum states)는 다음과 같습니다.

각각의 항들에 대한 의미는 다음과 같습니다.
먼저, 첫번째 항인 '2' 는 스핀 양자수를 의미합니다. 각 양자 상태는 2개의 스핀(spin state) 상태를 가질 수 있습니다.
두번째 항인 '1/8'은 제1팔분공간을 의미합니다. 즉, kx, ky, kz 가 모두 양수라고 고려한 것입니다.
세번째 항의 분자 '4πkdk'는 앞서 말씀드렸듯이 미소 부피(differential volume)입니다.
네번째 항의 분모 '(π/a)^3'는 하나의 양자 상태(quantum state)의 부피를 의미합니다.
식 (3.63)의 함수는 k(momentum)의 함수입니다. 이제 이를 변수를 치환하여 에너지의 함수로 변환하겠습니다.
식 (3.65b)와 식 (3.66)의 관계식을 통해 식 (3.63)을 에너지의 함수로 식 (3.68)과 같습니다.



식 (3.68)은 격자 상수(Lattice constant)가 a인 Cube 내의 에너지 (E,E+ΔE)에 존재하는 양자 상태의 총 수를 의미합니다.
따라서, 단위 부피당 양자 상태 밀도(the density of quantum states per unit volume of the crystal)는 다음과 같습니다.

긴 글 읽어주셔서 감사합니다.
'Semiconductor > Device Physics' 카테고리의 다른 글
| [물리전자] 3.5.2 페르미-디락 확률 함수(The Fermi-Dirac Probability Function) (0) | 2022.11.14 |
|---|---|
| [물리전자] 3.4.2 상태 밀도 함수(Density Of States Function) Ⅱ (0) | 2022.11.08 |
| [물리전자] 3.2.5 도체, 부도체, 반도체(Metal, Insulator, Semiconductor) (0) | 2022.10.31 |
| [물리전자] 3.2.4 정공(Hole)의 개념(Concept of the Hole) (0) | 2022.10.28 |
| [물리전자] 3.2.3 전자의 유효 질량(Electron Effective Mass) (2) | 2022.10.24 |




