| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Charge Carriers
- 앰비폴러 전송 방정식
- Density Of states function
- Excess Carrier
- 에너지밴드
- KANC
- Drift Current
- 서울 자치구별 경찰서
- 파동 함수
- Fermi Energy Level
- Diffusion Current
- 반도체공학
- 재결합(Recombination)
- 한국나노기술원
- Semiconductor
- 물리전자
- Mobility
- 확산 전류
- 나노분석평가
- Scattering
- 과잉 캐리어
- 캐리어 농도
- 생성(Generation)
- 페르미 에너지 준위
- 서울 경찰서 위도/경도
- neamen
- Ambipolar transport equation
- Energy Band
- 유효질량
- Wave Function
- Today
- Total
읽고 기록하는 삶
[물리전자] 3.2.4 정공(Hole)의 개념(Concept of the Hole) 본문
[물리전자] 3.2.4 정공(Hole)의 개념(Concept of the Hole)
늦더라도 확실하게 2022. 10. 28. 11:02
CHAPTER 3
Introduction to The Quantum Theory of Solids
3.2.4 Concept of the Hole
지난 글에서 유효 질량(Effective Mass)에 대해 알아보았습니다.
이번 글에서는 정공(Hole)의 정의와 정공(Hole)의 이동에 따른 전류에 대해 알아보겠습니다.
이전에 에너지 밴드 모델과 결합 모델을 다룰 때, Figure 3.17과 비슷하게 모델링 했던 거 기억 하시나요?
Figure 3.13a가 전자(electron) 관점에서의 모델링이라면 아래의 사진은 정공(Hole) 관점에서의 모델링입니다.
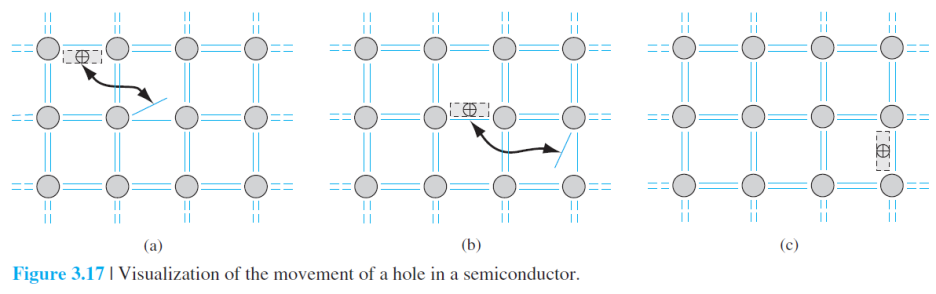
즉, T > 0K일 때, 가전자대(Valence Band)에서 충분한 에너지를 받은 전자가 전도대(Conduction band)로 여기하게 되면,
전자가 존재하던 공간은 그 자체로 (+) 전하를 띤 빈 상태(empty state)가 될 것입니다.
Figure 3.17은 그러한 움직임을 모델링한 그림이구요.
전자의 이동으로 인해 발생한 새로운 빈 상태(new empty state)를 정공(hole)이라고 정의하며, 이는 가전자대에서 거동합니다.
우리는 앞서 전자에 의한 표류 전류(Drift Current)를 다루면서 다음과 같이 표현되는 것을 학습하였습니다.
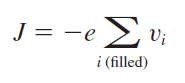
전류를 발생시킬 수 있는 Charge Carrier가 전자 말고 정공도 있다는 것을 확인하였으니, 다음과 같이 표현할 수 있습니다.
(The summation extends over all filled states. This summation is inconvenient since it extends over a nearly full valence band and takes into account a very large number of states. We may rewrite Equation (3.49) in the form)
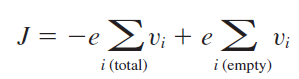
이 때, 에너지 밴드가 가득 찬 상태인 것으로 가정하면, 첫 번째 항의 값은 항상 0임을 알 수 있습니다.
(If we consider a band that is totally full, all available states are occupied by electrons. The individual electrons can be thought of as moving with a velocity as given by Equation (3.39). The band is symmetric in k and each state is occupied so that, for every electron with a velocity v , there is a corresponding electron with a velocity v . Since the band is full, the distribution of electrons with respect to k cannot be changed with an externally applied force. The net drift current density generated from a completely full band, then, is zero)
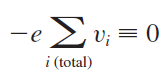
따라서, 전류 밀도는 정공의 관점에서 다음과 같이 표현될 수 있습니다.
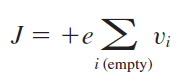
그렇다면 정공(Hole)의 유효 질량(Effective Mass)은 어떻게 표현할 수 있을까요?
바로 지난 글에서 다뤘던 내용과 동일한 방법으로 논리를 전개하면 쉽게 확인할 수 있습니다.
가전자대(Valence Band)의 E-K diagram을 2차 함수로 근사화 하면 다음과 같이 표현할 수 있습니다.
전도대(Conduction Band)의 E-K diagram을 근사화 한 것과의 차이점은 최고차항의 계수가 음수라는 것입니다.
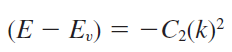
이제 앞서 했던 방법대로 동일하게 표현하면 정공(Hole)의 유효 질량을 다음과 같이 표현할 수 있습니다.
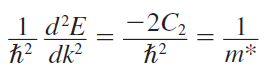
앞으로 정공에 대한 유효 질량은 m_p*로 표현하도록 하겠습니다.
이제 우리는 전자와 정공에 대한 유효 질량을 정의함으로써 보다 더 용이하게 문제를 해결할 수 있게 되었습니다.
다음 글에서는 도체와 부도체, 그리고 반도체에 대한 에너지 밴드를 간략하게 살펴보며 Chapter 3.2를 마무리 하겠습니다.
감사합니다.
'Semiconductor > Device Physics' 카테고리의 다른 글
| [물리전자] 3.4.1 상태 밀도 함수(Density Of States Function) (0) | 2022.11.03 |
|---|---|
| [물리전자] 3.2.5 도체, 부도체, 반도체(Metal, Insulator, Semiconductor) (0) | 2022.10.31 |
| [물리전자] 3.2.3 전자의 유효 질량(Electron Effective Mass) (2) | 2022.10.24 |
| [물리전자] 3.2.2 표류 전류(Drift Current) (0) | 2022.10.13 |
| [물리전자] 3.2.1 에너지 밴드와 원자가 결합 이론(The Bond Model) (0) | 2022.10.12 |




