| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 앰비폴러 전송 방정식
- 서울 경찰서 위도/경도
- Density Of states function
- Wave Function
- Ambipolar transport equation
- neamen
- 확산 전류
- 반도체공학
- 서울 자치구별 경찰서
- 에너지밴드
- Mobility
- 생성(Generation)
- KANC
- 물리전자
- 페르미 에너지 준위
- 캐리어 농도
- 유효질량
- 과잉 캐리어
- Diffusion Current
- 나노분석평가
- Excess Carrier
- Charge Carriers
- Energy Band
- 재결합(Recombination)
- Semiconductor
- Scattering
- Fermi Energy Level
- 한국나노기술원
- Drift Current
- 파동 함수
- Today
- Total
읽고 기록하는 삶
[물리전자] 3.2.3 전자의 유효 질량(Electron Effective Mass) 본문
[물리전자] 3.2.3 전자의 유효 질량(Electron Effective Mass)
늦더라도 확실하게 2022. 10. 24. 12:19
CHAPTER 3
Introduction to The Quantum Theory of Solids
3.2.3 Electron Effective Mass
지금까지 우리는 전자가 자유 공간 내에 존재한다고 가정하고 논리를 전개하며 학습하였습니다. 그러나, 대부분의 경우에 전자는 주변 환경의 영향을 받고 있는데요. 오늘은 관련 개념인 유효 질량(Effective Mass)을 다뤄보겠습니다.
전자(Electron)는 주변 환경의 영향을 받고 있습니다.
외부에서 가해지는 다양한 외력 뿐만 아니라, 결정(Crystal) 내의 양이온이나 중성자들도 전하에 영향을 주기 때문입니다.
이를 수식으로 표현하면 다음과 같습니다.

위의 식 (3.36)은 결정(Crystal) 내의 전자가 받는 힘을 표현한 것입니다. 즉, 전자는 외력(external force)와 내력(internal force)에 의해 운동합니다. 그러나, 내부의 힘을 모두 고려하며 전자의 거동을 표현하는 것은 매우 어렵기 때문에 유효질량(Effective mass)이라는 개념이 등장합니다.

위의 식 (3.37)에서 m*은 내부의 힘을 고려하여 새롭게 정의된 질량, 유효 질량(Effective Mass)을 의미합니다.
즉, 외력에 의한 영향만을 고려하여 전자의 거동을 보다 용이하게 해석하기 위해 도입한 것이라고 생각하시면 됩니다.
예를 들어, 물이 담긴 용기와 기름이 담긴 용기가 있다고 가정하겠습니다. 그리고, 동일한 두 물체를 각각의 용기에 넣는다고 가정해보죠. 당연하게도 물체는 아래로 가라앉게 될텐데, 이 때의 외력(External Force)은 중력이고, 내력(Internal Force)는 액체의 점도가 됩니다. 같은 외력(External Force)이지만 서로 다른 내부의 힘(Internal Force)으로 인하여 물체가 다른 거동을 하는 것을 알 수 있습니다.
그렇다면 새롭게 정의된 유효 질량(Effective Mass)은 어떻게 구할 수 있을까요?
자유 전자의 E-K diagram을 통해 유효 질량 m*을 알아보겠습니다.
우리는 앞서 에너지와 모멘텀의 관계를 이미 다뤄봤는데요. 이를 통해 E와 K의 관계식을 알 수 있습니다.

식 (3.28)을 양변을 k에 대해 미분하면 아래와 같습니다.

이것은 E-K diagram에서 곡선의 기울기는 해당 입자의 속도를 의미합니다.
그렇다면 한번 더 미분하면 어떨까요?

이것은 즉, E-K diagram에서의 곡률은 해당 입자의 질량에 반비례한다는 것을 알 수 있습니다.
이제, 지금까지의 내용을 바탕으로 유효 질량(Effective Mass)을 구해보겠습니다.
E-K diagram을 2차 함수로 근사화(Approximation)하여 논리를 전개하겠습니다. 다음 사진을 보시죠.

Figure 3.16a, Figure 3.16b은 전도대(Conduction Band)와 가전자대(Valence Band)의 E-K diagram을 근사화한 것입니다.
먼저, Figure 3.16a를 보겠습니다.
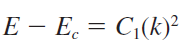
식 (3.44)는 전도대(Conduction Band)의 E-K diagram을 이차함수로 근사(approximation)한 것입니다.
이를 두 번 미분한 다음, 식 (3.41)을 활용하면 다음과 같은 식을 얻을 수 있습니다.

식 (3.41)과 식 (3.46)의 차이점을 아시겠나요?
식 (3.41)은 자유 전자일 때, 식 (3.46)은 보다 일반적인 상황에서 E-K diagram을 2차 함수로 근사화 했을 때의 관계식입니다.
즉, 식 (3.46)을 유효 질량(Effective Mass)을 활용하여 식 (3.41)의 형태로 표현하면 다음과 같습니다.

이러한 관계식을 통해 우리는 다양한 상황에서의 전자에 대한 질량을 유효 질량(Effective Mass)으로 편하게 표기할 수 있게 되었습니다. 앞으로 전자에 대한 유효 질량을 m_n*으로 표현하도록 하겠습니다.
지금까지 유효 질량(Effective Mass)의 의미와 구하는 방법에 대해 알아보았습니다.
다음 글에서는 정공(Hole)에 대한 개념 및 유효 질량(Effective Mass)을 알아보며 유효 질량 개념을 마무리 하겠습니다.
감사합니다.
'Semiconductor > Device Physics' 카테고리의 다른 글
| [물리전자] 3.2.5 도체, 부도체, 반도체(Metal, Insulator, Semiconductor) (0) | 2022.10.31 |
|---|---|
| [물리전자] 3.2.4 정공(Hole)의 개념(Concept of the Hole) (0) | 2022.10.28 |
| [물리전자] 3.2.2 표류 전류(Drift Current) (0) | 2022.10.13 |
| [물리전자] 3.2.1 에너지 밴드와 원자가 결합 이론(The Bond Model) (0) | 2022.10.12 |
| [물리전자] 3.1.1 에너지 밴드(Energy Band)의 형성 (1) | 2022.08.26 |




